Introduction
The most common types of ratemaking models in the insurance industry are frequency, severity, and pure premium models. Frequency models predict how often claims are made, and severity models predict claim amounts. The term pure premium is unique to insurance; it is the portion of the company’s expected cost that is “purely” attributed to loss. Pure premium does not include the general expense of doing business, such as overhead and commissions. Traditionally, the Tweedie distribution is used to model pure premium in a generalized linear model framework (GLM).
XGBoost has become incredibly popular on Kaggle in the last year for any problems dealing with structured data and accuracy predictions. Random forest was also incredibly popular on Kaggle few years ago. Let's play with both models using insurance data to model the pure premium.
Dataset description
- Dataset used in this code:
claim_history.csv - The
claim_history.csvdataset comes from the help library of SAS Enterprise-Miner version 7.1 - Data description:
- observations: 10302
- Variables: 27
Variable description:
| # | Variable | Label |
| 1 | ID | Identification# |
| 2 | KIDSDRIV | #Driving Children |
| 3 | BIRTH | Date of Birth |
| 4 | AGE | Age |
| 5 | HOMEKIDS | #Children @Home |
| 6 | YOJ | Years on Job |
| 7 | INCOME | Income |
| 8 | PARENT1 | Single Parent |
| 9 | HOME_VAL | Home Value |
| 10 | MSTATUS | Marital Status |
| 11 | GENDER | Driver Gender |
| 12 | EDUCATION | Max Education Level |
| 13 | OCCUPATION | Driver Occupation |
| 14 | TRAVTIME | Distance to Work |
| 15 | CAR_USE | Vehicle Use |
| 16 | BLUEBOOK | Value of Vehicle |
| 17 | TIF | Time in Force |
| 18 | CAR_TYPE | Type of Car |
| 19 | RED_CAR | A Red Car |
| 20 | OLDCLAIM | Total Claims(Past 5 Years) |
| 21 | CLM_FREQ | #Claims(Past 5 Years) |
| 22 | REVOKED | License Revoked (Past 7 Years) |
| 23 | MVR_PTS | Motor Vehicle Record Points |
| 24 | CLM_AMT | Claim Amount |
| 25 | CAR_AGE | Vehicle Age |
| 26 | CLAIM_FLAG | Claim Indicator |
| 27 | URBANICITY | Home/Work Area |
Getting and Preprocessing the Data
- Load packages and data
- Drop unuseful features
- Treatment of missing observations
- Transform some features from continuous to categorical
- Transform some categorical features into dummy variables
- Clean some new features names
- Scaling target variables
- Splitting the data into training, testing, and validation sets
Load packages and data
First load the needed packages:
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
import scipy as scipy
import pylab as pylab
import seaborn as sns
from xgboost import XGBRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error
%matplotlib inline
Next, load the CSV file as a Pandas data frame:
claims = pd.read_csv('data/claim_history.csv')
Let's take a look to the data:
claims.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 10302 entries, 0 to 10301
Data columns (total 27 columns):
ID 10302 non-null int64
KIDSDRIV 10302 non-null int64
BIRTH 10302 non-null object
AGE 10295 non-null float64
HOMEKIDS 10302 non-null int64
YOJ 9754 non-null float64
INCOME 9732 non-null object
PARENT1 10302 non-null object
HOME_VAL 9727 non-null object
MSTATUS 10302 non-null object
GENDER 10302 non-null object
EDUCATION 10302 non-null object
OCCUPATION 9637 non-null object
TRAVTIME 10302 non-null int64
CAR_USE 10302 non-null object
BLUEBOOK 10302 non-null object
TIF 10302 non-null int64
CAR_TYPE 10302 non-null object
RED_CAR 10302 non-null object
OLDCLAIM 10302 non-null object
CLM_FREQ 10302 non-null int64
REVOKED 10302 non-null object
MVR_PTS 10302 non-null int64
CLM_AMT 10302 non-null object
CAR_AGE 9663 non-null float64
CLAIM_FLAG 10302 non-null int64
URBANICITY 10302 non-null object
dtypes: float64(3), int64(8), object(16)
memory usage: 2.1+ MB
There are 27 columns. The target variable is CLM_AMT. Let's go deeper into the data:
claims.head()
| ID | KIDSDRIV | BIRTH | AGE | HOMEKIDS | YOJ | INCOME | PARENT1 | HOME_VAL | MSTATUS | ... | CAR_TYPE | RED_CAR | OLDCLAIM | CLM_FREQ | REVOKED | MVR_PTS | CLM_AMT | CAR_AGE | CLAIM_FLAG | URBANICITY | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 63581743 | 0 | 16MAR39 | 60.0 | 0 | 11.0 | $67,349 | No | $0 | z_No | ... | Minivan | yes | $4,461 | 2 | No | 3 | $0 | 18.0 | 0 | Highly Urban/ Urban |
| 1 | 132761049 | 0 | 21JAN56 | 43.0 | 0 | 11.0 | $91,449 | No | $257,252 | z_No | ... | Minivan | yes | $0 | 0 | No | 0 | $0 | 1.0 | 0 | Highly Urban/ Urban |
| 2 | 921317019 | 0 | 18NOV51 | 48.0 | 0 | 11.0 | $52,881 | No | $0 | z_No | ... | Van | yes | $0 | 0 | No | 2 | $0 | 10.0 | 0 | Highly Urban/ Urban |
| 3 | 727598473 | 0 | 05MAR64 | 35.0 | 1 | 10.0 | $16,039 | No | $124,191 | Yes | ... | z_SUV | no | $38,690 | 2 | No | 3 | $0 | 10.0 | 0 | Highly Urban/ Urban |
| 4 | 450221861 | 0 | 05JUN48 | 51.0 | 0 | 14.0 | NaN | No | $306,251 | Yes | ... | Minivan | yes | $0 | 0 | No | 0 | $0 | 6.0 | 0 | Highly Urban/ Urban |
5 rows × 27 columns
Convert some features from currency to float
Now it is clear that some interval features such INCOME or HOME_VAL have a currency format. Therefore, we need to convert currency to float:
# From currency to float
for field in ['INCOME', 'HOME_VAL', 'BLUEBOOK', 'OLDCLAIM', 'CLM_AMT']:
claims.loc[:,field] = claims[field] = (claims[field].replace( '[\$,)]','', regex=True )
.replace( '[(]','-', regex=True ).astype(float))
Drop unuseful features
There are some variables that are unuseful in this context, we can drop them:
claims = claims.drop(['ID','BIRTH','CLAIM_FLAG'], axis=1)
Treatment of missing observations
Let's take a look to the missing observations:
claims.isnull().sum()
KIDSDRIV 0
AGE 7
HOMEKIDS 0
YOJ 548
INCOME 570
PARENT1 0
HOME_VAL 575
MSTATUS 0
GENDER 0
EDUCATION 0
OCCUPATION 665
TRAVTIME 0
CAR_USE 0
BLUEBOOK 0
TIF 0
CAR_TYPE 0
RED_CAR 0
OLDCLAIM 0
CLM_FREQ 0
REVOKED 0
MVR_PTS 0
CLM_AMT 0
CAR_AGE 639
URBANICITY 0
dtype: int64
There are some variables with few missing observations. The features YOJ,INCOME, HOME_VAL and CAR_AGE are interval features, it is easy to replace the missed observations with the mean of the variable:
# Inputation for interval features
for field in ['AGE','YOJ','INCOME','HOME_VAL','CAR_AGE']:
claims.loc[:,field] = claims.fillna(claims.mean()[field])
the OCCUPATION column is categorical. In order to fill NaNs with the most frequent value from the categorical OCCUPATION column:
claims = claims.fillna(claims['OCCUPATION'].value_counts().index[0])
Transform some features from continuous to categorical
The following features KIDSDRIV, HOMEKIDS and CLM_FREQ are continuous in our dataset. We need to convert this variables into a string type because has no sense to treat these variables as continuous:
claims[['KIDSDRIV','HOMEKIDS','CLM_FREQ']] = claims[['KIDSDRIV','HOMEKIDS','CLM_FREQ']].astype(str)
Transform some categorical features into dummy variables
Here we have some categorical variables like KIDSDRIV or CAR_TYPE. To include these in our model, we'll need to make dummy variables. This is simple to do with Pandas thanks to get_dummies().
dummy_fields = ['KIDSDRIV','HOMEKIDS','PARENT1','MSTATUS','GENDER','EDUCATION',\
'OCCUPATION','CAR_USE','CAR_TYPE','RED_CAR','CLM_FREQ','REVOKED',\
'URBANICITY']
for each in dummy_fields:
dummies = pd.get_dummies(claims[each], prefix=each, drop_first=False)
claims = pd.concat([claims, dummies], axis=1)
fields_to_drop = ['KIDSDRIV','HOMEKIDS','PARENT1','MSTATUS','GENDER','EDUCATION',\
'OCCUPATION','CAR_USE','CAR_TYPE','RED_CAR','CLM_FREQ','REVOKED',\
'URBANICITY']
claims = claims.drop(fields_to_drop, axis=1)
Let's check how many variables we have now:
claims.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 10302 entries, 0 to 10301
Data columns (total 61 columns):
AGE 10302 non-null float64
YOJ 10302 non-null float64
INCOME 10302 non-null float64
HOME_VAL 10302 non-null float64
TRAVTIME 10302 non-null int64
BLUEBOOK 10302 non-null float64
TIF 10302 non-null int64
OLDCLAIM 10302 non-null float64
MVR_PTS 10302 non-null int64
CLM_AMT 10302 non-null float64
CAR_AGE 10302 non-null float64
KIDSDRIV_0 10302 non-null uint8
KIDSDRIV_1 10302 non-null uint8
KIDSDRIV_2 10302 non-null uint8
KIDSDRIV_3 10302 non-null uint8
KIDSDRIV_4 10302 non-null uint8
HOMEKIDS_0 10302 non-null uint8
HOMEKIDS_1 10302 non-null uint8
HOMEKIDS_2 10302 non-null uint8
HOMEKIDS_3 10302 non-null uint8
HOMEKIDS_4 10302 non-null uint8
HOMEKIDS_5 10302 non-null uint8
PARENT1_No 10302 non-null uint8
PARENT1_Yes 10302 non-null uint8
MSTATUS_Yes 10302 non-null uint8
MSTATUS_z_No 10302 non-null uint8
GENDER_M 10302 non-null uint8
GENDER_z_F 10302 non-null uint8
EDUCATION_<High School 10302 non-null uint8
EDUCATION_Bachelors 10302 non-null uint8
EDUCATION_Masters 10302 non-null uint8
EDUCATION_PhD 10302 non-null uint8
EDUCATION_z_High School 10302 non-null uint8
OCCUPATION_Clerical 10302 non-null uint8
OCCUPATION_Doctor 10302 non-null uint8
OCCUPATION_Home Maker 10302 non-null uint8
OCCUPATION_Lawyer 10302 non-null uint8
OCCUPATION_Manager 10302 non-null uint8
OCCUPATION_Professional 10302 non-null uint8
OCCUPATION_Student 10302 non-null uint8
OCCUPATION_z_Blue Collar 10302 non-null uint8
CAR_USE_Commercial 10302 non-null uint8
CAR_USE_Private 10302 non-null uint8
CAR_TYPE_Minivan 10302 non-null uint8
CAR_TYPE_Panel Truck 10302 non-null uint8
CAR_TYPE_Pickup 10302 non-null uint8
CAR_TYPE_Sports Car 10302 non-null uint8
CAR_TYPE_Van 10302 non-null uint8
CAR_TYPE_z_SUV 10302 non-null uint8
RED_CAR_no 10302 non-null uint8
RED_CAR_yes 10302 non-null uint8
CLM_FREQ_0 10302 non-null uint8
CLM_FREQ_1 10302 non-null uint8
CLM_FREQ_2 10302 non-null uint8
CLM_FREQ_3 10302 non-null uint8
CLM_FREQ_4 10302 non-null uint8
CLM_FREQ_5 10302 non-null uint8
REVOKED_No 10302 non-null uint8
REVOKED_Yes 10302 non-null uint8
URBANICITY_Highly Urban/ Urban 10302 non-null uint8
URBANICITY_z_Highly Rural/ Rural 10302 non-null uint8
dtypes: float64(8), int64(3), uint8(50)
memory usage: 1.4 MB
Now we have 61 variables in our dataset.
Clean some new features names
The XGBoost and the random forest algorithms don't admit special symbols in the feature names such as <> or / or ,. Therefore, we need to rename those feature names:
claims = claims.rename(columns={'EDUCATION_<High School': 'EDUCATION_lt_High_School',
'OCCUPATION_z_Blue Collar': 'OCCUPATION_z_Blue_Collar',
'CAR_TYPE_Panel Truck': 'CAR_TYPE_Panel_Truck',
'CAR_TYPE_Sports Car': 'CAR_TYPE_Sports_Car',
'URBANICITY_Highly Urban/ Urban': 'URBANICITY_Urban',
'URBANICITY_z_Highly Rural/ Rural': 'URBANICITY_Rural'})
plot_clm_amt = claims['CLM_AMT']
Scaling target variables
To make training the network easier, we'll standardize each of the continuous variables. That is, we'll shift and scale the variables such that they have zero mean and a standard deviation of 1.
The scaling factors are saved so we can go backwards when we use the network for predictions.
quant_features = ['AGE', 'YOJ', 'INCOME', 'HOME_VAL',
'BLUEBOOK', 'OLDCLAIM', 'CLM_AMT', 'CAR_AGE']
# Store scalings in a dictionary so we can convert back later
scaled_features = {}
for each in quant_features:
mean, std = claims[each].mean(), claims[each].std()
scaled_features[each] = [mean, std]
claims.loc[:, each] = (claims[each] - mean)/std
Splitting the data into training, testing, and validation sets
We'll save the data for the last approximately 21 days to use as a test set after we've trained the network. We'll use this set to make predictions and compare them with the actual number of riders.
# Split off random 50% of the data for training, 25% for testing and 25% for validation
np.random.seed(21)
sample = np.random.choice(claims.index, size=int(len(claims)*0.5), replace=False)
data, train = claims.ix[sample], claims.drop(sample)
sample = np.random.choice(data.index, size=int(len(data)*0.5), replace=False)
val, test = data.ix[sample], data.drop(sample)
# Split into features and targets
features, targets = train.drop('CLM_AMT', axis=1), train['CLM_AMT']
features_val, targets_val = val.drop('CLM_AMT', axis=1), val['CLM_AMT']
features_test, targets_test = test.drop('CLM_AMT', axis=1), test['CLM_AMT']
With this we've finished the data preparation tasks, we are ready to use XGBoost and random forest.
Fitting the model
Let's fit the XGBoost and the random forest to the data:
# fit XGBoost model to training data
xgb_model = XGBRegressor()
xgb_model.fit(features, targets)
XGBRegressor(base_score=0.5, colsample_bylevel=1, colsample_bytree=1, gamma=0,
learning_rate=0.1, max_delta_step=0, max_depth=3,
min_child_weight=1, missing=None, n_estimators=100, nthread=-1,
objective='reg:linear', reg_alpha=0, reg_lambda=1,
scale_pos_weight=1, seed=0, silent=True, subsample=1)
# fit random forest to training data
rf_model = RandomForestRegressor(200)
rf_model.fit(features, targets)
RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None,
max_features='auto', max_leaf_nodes=None,
min_impurity_split=1e-07, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
n_estimators=200, n_jobs=1, oob_score=False, random_state=None,
verbose=0, warm_start=False)
Make predictions for the test data
We are now ready to use the trained model to make predictions. We can make predictions using the fit model on the test dataset. To make predictions we use the scikit-learn function model.predict().
# make predictions for test data using XGBoost
y_pred_xgb = xgb_model.predict(features_test)
#predictions = [round(value ,2) for value in y_pred]
# make predictions for test data using random forest
y_pred_rf = rf_model.predict(features_test)
#predictions = [round(value ,2) for value in y_pred]
Evaluate model performance
Now that we have used the fit model to make predictions on new data, we can evaluate the performance of the predictions by comparing them to the expected values. For this we will use the built in mean_absolute_error function in scikit-learn.
# evaluate predictions using XGBoost
score = mean_absolute_error(targets_test, y_pred_xgb)
print("XGBoost Score: %.4f" % score)
XGBoost Score: 0.4036
# evaluate predictions using random forest
score = mean_absolute_error(targets_test, y_pred_rf)
print("Random forest Score: %.4f" % score)
Random forest Score: 0.4297
It is clear that the XGBoost fits the data better than the random forest. The absolute mean error is lower for the XGBoost. Let's go deeper and create a lift chart to compare the model performance from another point of view.
Create a lift chart to compere model performance
A classical chart used to compere regressions models (also classification) is a Lift chart. Let's create both lift charts.
def gini(actual,pred,weight=None):
pdf= pd.DataFrame(scipy.vstack([actual,pred]).T,columns=['Actual','Predicted'],)
pdf= pdf.sort_values('Predicted')
if weight is None:
pdf['Weight'] = 1.0
pdf['CummulativeWeight'] = np.cumsum(pdf['Weight'])
pdf['CummulativeWeightedActual'] = np.cumsum(pdf['Actual']*pdf['Weight'])
TotalWeight = sum(pdf['Weight'])
Numerator = sum(pdf['CummulativeWeightedActual']*pdf['Weight'])
Denominator = sum(pdf['Actual']*pdf['Weight']*TotalWeight)
Gini = 1.0 - 2.0 * Numerator/Denominator
return Gini
gini(targets_test,y_pred_xgb,weight=None)
-13.489679386152188
gini(targets_test,y_pred_rf,weight=None)
-13.082823959818159
def mylift(actual,pred,weight=None,n=10,xlab='Predicted Decile',MyTitle='Model Performance Lift Chart'):
pdf= pd.DataFrame(scipy.vstack([actual,pred]).T,columns=['Actual','Predicted'],)
pdf= pdf.sort(columns='Predicted')
if weight is None:
pdf['Weight'] = 1.0
pdf['CummulativeWeight'] = np.cumsum(pdf['Weight'])
pdf['CummulativeWeightedActual'] = np.cumsum(pdf['Actual']*pdf['Weight'])
TotalWeight = sum(pdf['Weight'])
Numerator = sum(pdf['CummulativeWeightedActual']*pdf['Weight'])
Denominator = sum(pdf['Actual']*pdf['Weight']*TotalWeight)
Gini = 1.0 - 2.0 * Numerator/Denominator
NormalizedGini = Gini/ gini(pdf['Actual'],pdf['Actual'])
GiniTitle = 'Normalized Gini = '+ str(round(NormalizedGini,4))
pdf['PredictedDecile'] = np.round(pdf['CummulativeWeight']*n /TotalWeight + 0.5,decimals=0)
pdf['PredictedDecile'][pdf['PredictedDecile'] < 1.0] = 1.0
pdf['PredictedDecile'][pdf['PredictedDecile'] > n] = n
pdf['WeightedPrediction'] = pdf['Predicted']*pdf['Weight']
pdf['WeightedActual'] = pdf['Actual']*pdf['Weight']
lift_df = pdf.groupby('PredictedDecile').agg({'WeightedPrediction': np.sum,'Weight':np.sum,'WeightedActual':np.sum,'PredictedDecile':np.size})
nms = lift_df.columns.values
nms[1] = 'Count'
lift_df.columns = nms
lift_df['AveragePrediction'] = lift_df['WeightedPrediction']/lift_df['Weight']
lift_df['AverageActual'] = lift_df['WeightedActual']/lift_df['Weight']
lift_df['AverageError'] = lift_df['AverageActual']/lift_df['AveragePrediction']
d = pd.DataFrame(lift_df.index)
p = lift_df['AveragePrediction']
a = lift_df['AverageActual']
pylab.plot(d,p,label='Predicted',color='blue',marker='o')
pylab.plot(d,a,label='Actual',color='red',marker='d')
pylab.legend(['Predicted','Actual'], loc=2)
pylab.title(MyTitle +'\n'+GiniTitle)
pylab.xlabel(xlab)
pylab.ylabel('Actual vs. Predicted')
pylab.grid()
pylab.show()
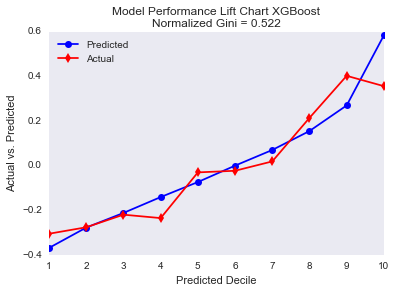
mylift(targets_test,y_pred_xgb,weight=None,n=10,xlab='Predicted Decile',\
MyTitle='Model Performance Lift Chart XGBoost')
mylift(targets_test,y_pred_rf,weight=None,n=10,xlab='Predicted Decile',\
MyTitle='Model Performance Lift Chart Random Forest')
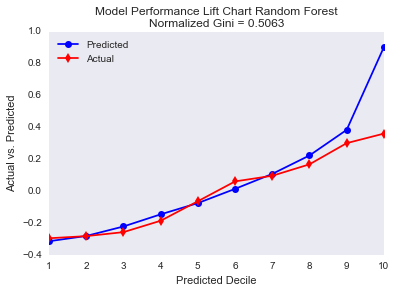
Although the random forest fits the data better than the XGBoost for the first nine percentiles, the XGBoost fits much better the tenth percentile. This is interesting because fitting a risk premium model is quite difficult because the great majority of the policies has no claim and therefore, the loss is zero as you can see in this image:
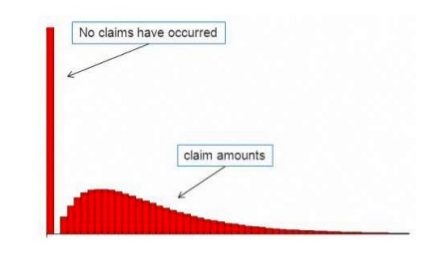
The policies with positive claims are mainly in the tenth decile. The random forest performs really bad for the policies with positive claims.
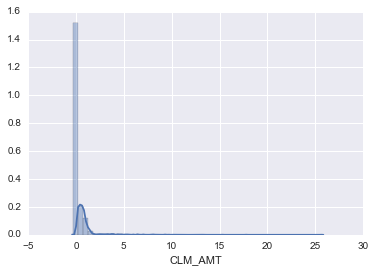
Here we can see the distribution of the risk premium in our dataset:
sns.distplot(plot_clm_amt)
<matplotlib.axes._subplots.AxesSubplot at 0x1216f0990>